Как работает инструмент Получить непрерывный поток

Доступно с Image Server

Понимание того, как вода течет по ландшафту после выпадения в виде осадков является основой для множества процессов. Цифровая модель рельефа (ЦМР) - базовый набор данных для моделирования потока по поверхности. Но эти данные частно не идеальны — в них могут быть некоторые неточности в высотах или небольшие искажения, которые, тем не менее, могут повлиять вычисление прохождения потока.

Поэтому входная ЦМР нуждается в предварительной обработке перед моделированием направления стока. Гидрологическая корректность основана на попытках изменения значений высот входной ЦМР для обеспечения непрерывной поверхности, формирующий сток, соответствующий реальному потоку по поверхности. Гидрологическая корректность исключает участки, в которых из-за особенностей ЦМР нарушается сеть водотоков, например, ложные значения высот определяются как локальные понижения и вызывают некорректную остановку потока, что делает невозможным определение направления стока наружу из ячеек понижения. Мосты, плотины и дренажные сооружения, не включенные в модель поверхности, так же могут способствовать ошибочным результатам расчета направления и накопления стока.

Инструмент Получить непрерывный поток исправляет ошибочные расчеты направления стока и суммарного стока, используя алгоритм пути с наименьшей стоимостью, не меняя при этом входные данные ЦМР. Алгоритм пути с наименьшей стоимостью использует минимизацию перепадов высот при перемещении в гору по входному растру поверхности. Другими словами, требуется оптимизированный шаг по принципу «ячейка-за-ячейкой» для определения соседа с наименьшим перепадом высот. Также применяются специальные правила для ячеек понижений и NoData. Ячейки, обозначающие понижения или впадины, могут быть одиночными или представлять собой группу ячеек, соседи которых имеют значения высот существенно выше, чем эта ячейка или группа ячеек. Ячейки NoData считаются ячейками, не имеющими информацию, и не используются при обработке.

Этот инструмент использует ЦМР в качестве входной поверхности и создает растр с информацией о направлении стока и суммарном стоке для каждой ячейки.

Если входной растр поверхности содержит истинные локальные понижения или впадины, их необходимо указать в параметре Входные растровые или векторные данные понижений. Если указан набор растровых данных, соответствующие ячейки входного растра будут определены как истинные ячейки понижений. Если указан набор векторных данных, объекты будут растеризованы с тем же разрешением, что и входные данные поверхности, и результирующий растр будет использован для определения истинных понижений.

Инструмент предлагает два метода определения направления стока в параметре Тип направления стока: Метод D8 моделирует направление стока из каждой ячейки в сторону соседней ячейки с максимальным перепадом высот, с ограничением до одного направления (Jenson and Domingue, 1988). Алгоритм Множественные направления стока (MFD), описанный разделяет сток по всем соседним ячейкам, которые расположены ниже по склону, что позволяет адаптировать сток в зависимости от локальных особенностей поверхности. (Qin et al., 2007).

Если указан Входной растр суммарных весов к каждой ячейке при расчете суммарного стока применяется вес.

Вычисление направления стока и суммарного стока

В алгоритме инструмента Получить непрерывный поток используются два базовых шага при вычислении пути с наименьшей стоимостью, и построении маршрута потока по поверхности. Сначала определяются истинные точки стока Это ячейки, в которые вода может стекать, но не может вытекать. По умолчанию эти ячейки расположены по краям входного растра поверхности. Если указаны Входные растровые или векторные данные понижений, соответствующие ячейки входного растра будут также отмечены как истинные точки стока перед запуском алгоритма. Следующий шаг - трассировка входного растра поверхности и получение направления стока и суммарного стока в каждой ячейке путем обработки ячеек в порядке от минимальной высоты к максимальной высоте. Эти два шага позволяет идентифицировать движение из текущей ячейки к следующей, более высокой ячейки в направлении наименьшего подъема в окрестности (Metz et al., 2011; Ehlschlaeger, 1989).

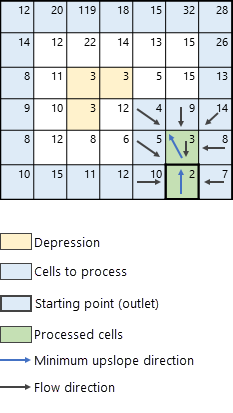
На следующем рисунке показана основная логика процесса. Специальные случаи, такие как впадины (локальные понижения), которые не определены как понижения в параметре Входные растровые или векторные данные понижений и ячейки NoData описываются в разделах Обработка неизвестных понижений и Ячейки NoData во входном растре поверхности соответственно.

Рис 1. Алгоритм пути с наименьшей стоимостью для определения маршрута потока и суммарного стока, описанный Metz et al., 2011; Ehlschlaeger, 1989, is shown.

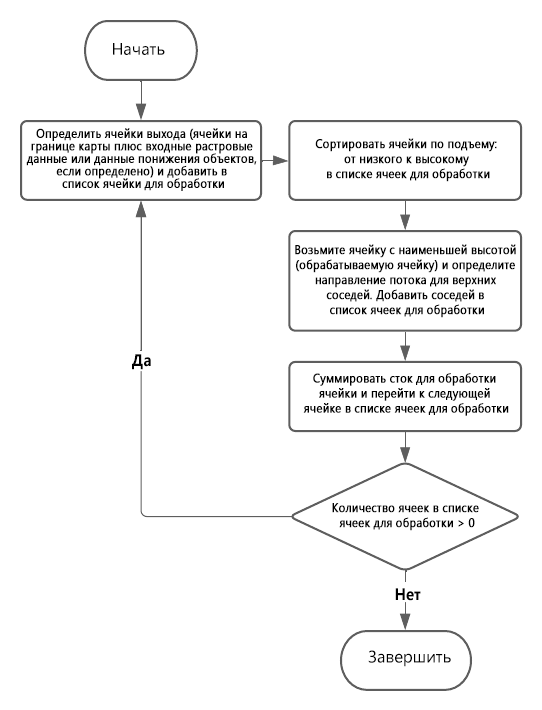
Логика инструмента Получить непрерывный поток

В этом разделе пошагово описан пример работы инструмента Получить непрерывный поток, включая обработку данных рельефа и определение направления потока и суммарного стока по принципу "ячейка за ячейкой". В этом примере присутствуют локальные понижения, которые не указаны в дополнительном параметре Входные растровые или векторные данные понижений (см. Рис 2).

Рис 2. В примере используется искусственная поверхность высот, с размером ячейки, равным 1. В используемой растровой поверхности присутствует впадина в центральной области, показанная желтым цветом, которая не обозначена в параметре Входные растровые или векторные данные понижений.

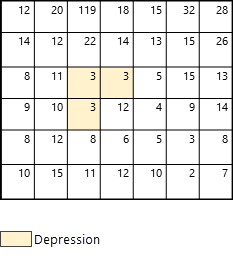
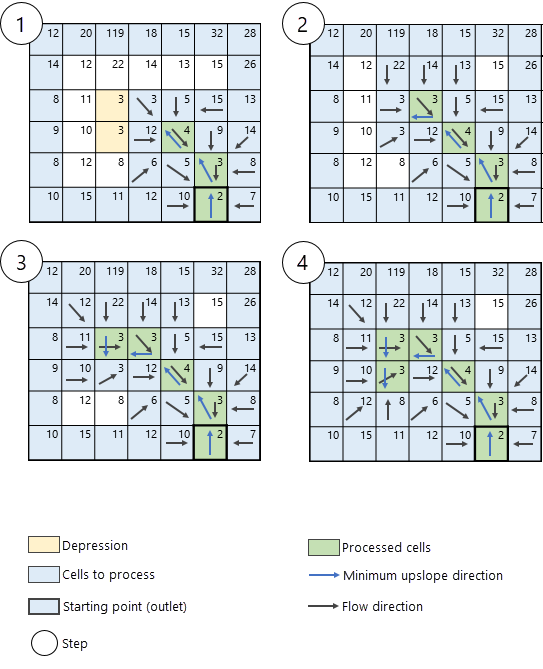
Сначала определяются ячейки истинных точек стока. Они соответствуют ячейкам по краям карты (показаны синим цветом на Рис. 3).

Рис. 3. Показаны ячейки точек стока, определенные как кандидаты в шаге 1.

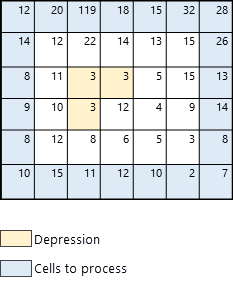
После определения ячеек точек стока (ячейки синего цвета), алгоритм переходит к поиску ячейки с наименьшей высотой, с которой начнется поиск. В примере ячейка с наименьшей высотой (значение 2) выделена толстым черным контуром на Рис. 4.

Рис. 4. В шаге 2 начальная точка идентифицируется через сортировку возможных ячеек точек стока по высоте и выбором ячейки с наименьшей высотой, выделенной толстым контуром черного цвета.

В следующем шаге идентифицируются соседи обрабатываемой ячейки (показаны зеленым цветом), чьи значения высоты больше обрабатываемой ячейки. Эти ячейки добавляются к пулу возможных ячеек, которые могут быть обработаны далее. Следующая ячейка для обработки определяется нахождением ячейки с наименьшей высотой выше по склону в окрестности (в этом примере ячейка со значением высоты - 3), соответствующая направлению в сторону минимального подъема (стрелка синего цвета на Рис. 5). Последовательно вычисляются направление стока и суммарный сток в окрестности выше по склону для обрабатываемой ячейки. Направление стока вычисляется по методу, указанному в параметре Тип направления стока. Есть два метода расчета направления стока, D8 и MFD. Подробное описание этих двух методов см. в разделе Методы расчета направления стока ниже.

Рис. 5. В шаге 3 идентифицируются ячейки в окрестности текущей обрабатываемой ячейки. Ячейки, выделенные синим цветом - кандидаты на обработку в следующем шаге. Черные стрелки соответствуют направлению стока, голубыми стрелками показан путь к следующей ячейке для обработки.

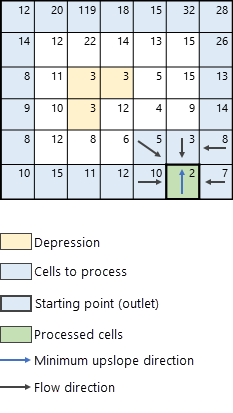
Алгоритм продолжается по тому же принципу, идентифицируя ячейки в окрестности текущей ячейки обработки в направлении минимального перепада высот. Следующая итерация алгоритма показана на Рис. 6.

Рис. 6. Следующая итерация. Как и на Рис 5, ячейки, выделенные синим цветом - кандидаты на обработку в следующем шаге. Следующая ячейка для обработки на схеме - 3, зеленого цвета. Черные стрелки соответствуют направлению стока, голубыми стрелками показано направление по пути с наименьшей стоимостью.

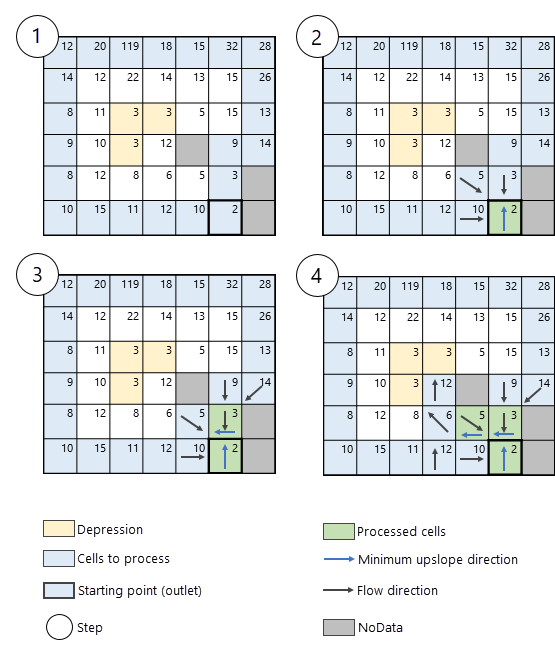
Обработка неизвестных ячеек понижений

Ячейки понижений или впадин, могут быть одиночными или представлять собой группу ячеек, соседи которых имеют значения высот существенно выше, чем эта ячейка или группа ячеек. Если они не определены в параметре Входные растровые или векторные данные понижений, они являются неизвестными понижениями для инструмента. Согласно сценарию, если встречается неизвестная ячейка или группа ячеек понижения (впадины), поток следует по самому крутому спуску (вместо того, чтобы следовать в направлении соседней ячейкой с минимальным подъемом), пока не достигнет дна впадины, установив направление стока и суммарный сток вдоль пути к впадине. Процесс показан на Рис. 7.

Рис.7 Показана последовательность обработки каждой ячейки в пределах впадины, слева направо. Направление стока и суммарный сток определяются для каждой ячейки внутри впадины. Направление обработки через впадину ячейке с самым крутым спуском, вместо ячейки с минимальным подъемом в окрестности.

Ячейки NoData во входном растре поверхности

Ячейки NoData во входном растре поверхности - это ячейки, значения которых неизвестны. Эти ячейки могут присутствовать в растре поверхности и могут быть выявлены алгоритмом получения непрерывного потока. Если такая ячейка встречается, она не обрабатывается, и алгоритм проходит сквозь нее, как показано на Рис. 8.

Рис. 8 Ячейки NoData во входном растре поверхности игнорируются инструментом Получить непрерывный поток Внешние ячейки NoData сдвигают границы входного растра поверхности к окрестности с корректными значениями данных. В оставшихся ячейках вычисления для определения направления стока и суммарного стока остаются без изменений.

Методы расчета Направления стока

В методе D8 направление стока определяется направлением наиболее крутого спуска, или максимального понижения, из каждой ячейки (Jenson and Domingue, 1988). Оно вычисляется следующим образом:

maximum_drop = change_in_z-value/distance

Расстояние вычисляется между центрами ячеек. Для угловых соседних ячеек алгоритм проверяет, что максимальное понижение в направлении текущей обрабатываемой ячейки является максимальным; в противном случае направление потока будет установлено в сторону ячейки с максимальным понижением данной угловой соседней ячейки. Если для ячейки характерно одно и то же изменение в z-значении в нескольких направлениях, направление стока D8 неопределено, и значением будет сумма возможных направлений.

Если найдено направление самого крутого понижения, выходной ячейке дается значение, представляющее это направление.

По методу MFD сток распределяется по всем соседям ниже по склону (Qin et al., 2007). Количество стока, получаемого каждым соседом по склону, оценивается как функция максимального уклона склона, что позволяет учитывать локальные условия рельефа. Выражение для оценки MFD выглядит следующим образом:

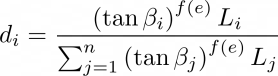
Где:

• d_i = Часть стока из каждой ячейки, которая поступает в ячейку i
• f (e) = Показатель степени, который адаптируется к локальным условиям рельефа, задается

  

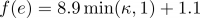
• β = Угол уклона (в радианах)
• n = количество ячеек, которое поступает в ячейку i
• L_i, L_j = Скорректированный коэффициент для учета расстояния между обрабатываемой ячейкой и ортогональными и диагональными ячейками
• κ = Максимальное понижение по ячейкам, которое поступает в ячейку i

После определения направления стока и суммарного стока, а также направления по пути с наименьшей стоимостью, обрабатываемая ячейка помечается как обработанная, и намечается следующая ячейка для анализа. Алгоритм применяется таким же образом, до тех пор, пока все ячейки входного растра поверхности не будут обработаны. Другими словами, направление стока и суммарный сток вычисляются для всех ячеек.

Список литературы

Ehlschlaeger, C. R. 1989. "Using the AT Search Algorithm to Develop Hydrologic Models from Digital Elevation Data." International Geographic Information Systems (IGIS) Symposium 89: 275-281.

Jenson, S. K., and Domingue, J. O. 1988. "Extracting Topographic Structure from Digital Elevation Data for Geographic Information System Analysis." Photogrammetric Engineering and Remote Sensing 54 (11): 1593–1600.

Metz, M., Mitasova, H., & Harmon, R. S. 2011. "Efficient extraction of drainage networks from massive, radar-based elevation models with least cost path search." Hydrology and Earth System Sciences 15(2): 667-678.

Qin, C., Zhu, A. X., Pei, T., Li, B., Zhou, C., & Yang, L. 2007. "An adaptive approach to selecting a flow partition exponent for a multiple flow direction algorithm." International Journal of Geographical Information Science 21(4): 443-458.