ポイントの集約、エリア内での集計、近接範囲内での集計、フィーチャの結合、境界のディゾルブの各ツールによって統計サマリーが計算されます。
方程式
平均と標準偏差の計算には、ライン フィーチャとポリゴン フィーチャの加重平均および加重標準偏差を使用します。 ポイント フィーチャの統計は重み付けされません。 加重は、境界内にあるフィーチャの長さまたは面積です。
標準偏差、加重平均、および加重標準偏差の計算に使用される方程式を次の表に示します。
| 統計 | 方程式 | 変数 | フィーチャ |
|---|---|---|---|
標準偏差 |  | 条件:
| ポイント |
加重平均 |  | 条件:
| ラインとポリゴン |
加重標準偏差 |  | 条件:
| ラインとポリゴン |
注意:
すべての統計計算から NULL 値が除外されます。 たとえば、10、5、および NULL 値の平均値は
7.5 です ((10+5)/2)。ポイント
ポイント レイヤーの集計には、境界エリア内にあるポイント フィーチャのみを使用します。
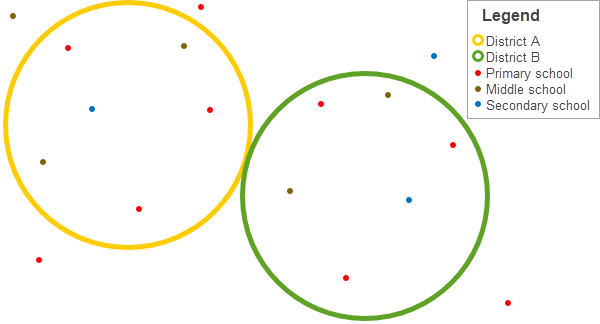
ポイント集計の実用例として、それぞれの学区内の学生の合計人数を調べることが挙げられます。 各ポイントは 1 つの学校を表します。 Type フィールドには、学校の種類 (小学校、中学校、または高校) が示され、人口のフィールドには、各学校に入学した学生の人数が示されています。
次の図は仮想的なポイントと境界レイヤーを示したものであり、表ではポイント レイヤーの属性が集計されています。
| ObjectID | 地区 | タイプ | 人口 |
|---|---|---|---|
1 | A | Primary school | 280 |
2 | A | Primary school | 408 |
3 | A | Primary school | 356 |
4 | A | Middle school | 361 |
5 | A | Middle school | 450 |
6 | A | Secondary school | 713 |
7 | B | Primary school | 370 |
8 | B | Primary school | 422 |
9 | B | Primary school | 495 |
10 | B | Middle school | 607 |
11 | B | Middle school | 574 |
12 | B | Secondary school | 932 |
地区 A の計算と結果は以下の表のとおりです。 この結果から、地区 A には 2,568 人の学生が存在していることがわかります。 ツールを実行すると、地区 B の結果も表示されます。
| 統計 | 地区 A の結果 |
|---|---|
合計 | |
最小 | 次のうちの最小: |
最大 | 次のうちの最大: |
平均 | |
標準偏差 | |
ライン
ライン レイヤーの集計には、境界エリア内にあるライン フィーチャの比率のみを使用します。
ヒント:
ラインを集計する場合は、数や量を持つフィールドを使用して、比率計算が解析で論理的な意味を持つようにします。 たとえば、人口密度の代わりに人口を使用します。
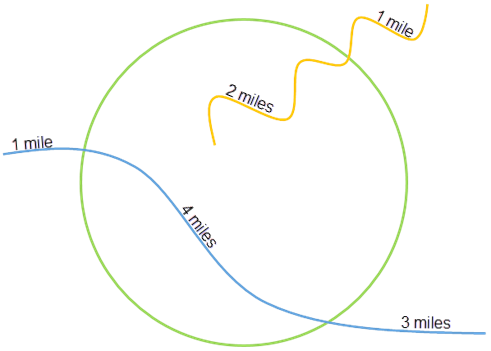
この解析の実用例では、指定した境界内にある河川の合計水量を算出します。 各ラインは、境界内に流域の一部が存在する河川を表しています。
次の図は仮想的なラインと境界レイヤーを示したものであり、表ではライン レイヤーの属性が集計されています。
| 川 | 長さ (マイル) | 水量 (ガロン) |
|---|---|---|
黄 | 3 | 6,000 |
青 | 8 | 10,000 |
水量の計算は以下の表のとおりです。 この結果から、合計水量が 9,000 ガロンであることがわかります。
注意:
この計算では、境界エリア内のラインの比率を使用しています。 たとえば、黄色いラインの合計水量は 6,000 ガロンで、3 つの合計マイルのうち 2 つが境界内にあります。 そのため、黄色いラインの水量として 4,000 ガロンを使用して計算が実行されます。
6000*(2/3)=4000| 統計 | 結果 |
|---|---|
合計 | |
最小 | 次のうちの最小: |
最大 | 次のうちの最大: |
平均 | |
標準偏差 | |
ポリゴン
ポリゴン レイヤーの集計には、境界エリア内にあるポリゴン フィーチャの比率のみを使用します。
ヒント:
ポリゴンを集計する場合は、数や量を持つフィールドを使用して、比率計算が解析で論理的な意味を持つようにします。 たとえば、人口密度の代わりに人口を使用します。
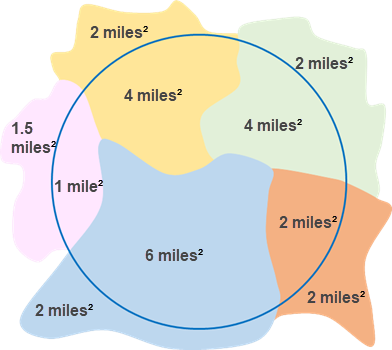
この解析の実用例は、都市近郊の人口を算出する場合です。 青のアウトラインは近郊との境界を表し、小さいポリゴンは国勢調査区を表しています。
次の図は仮想的なポリゴンと境界レイヤーを示したものであり、表ではポリゴン レイヤーの属性が集計されています。
| 国勢調査ブロック | 面積 (平方マイル) | 人口 |
|---|---|---|
黄 | 6 | 3,200 |
緑 | 6 | 4,700 |
ピンク | 2.5 | 1,000 |
青 | 8 | 4,500 |
オレンジ | 4 | 3,600 |
人口の計算は以下の表のとおりです。 この結果から、近郊に 10,841 人が居住しており、国勢調査区当たりの平均人口は約 2,666 人であることがわかります。
注意:
この計算では、境界エリア内のポリゴンの比率を使用しています。 たとえば、黄色いポリゴンの合計人口は 3,200 人で、6 つの合計平方マイルのうち 4 つが境界内にあります。 そのため、黄色いポリゴンの人口として 2,133 を使用して計算が実行されます。
3200*(4/6)=2133| 統計 | 結果 |
|---|---|
合計 | |
最小 | 次のうちの最小: |
最大 | 次のうちの最大: |
平均 | |
標準偏差 | |
関連トピック
以下のトピックを参照して、特定のツール内の統計サマリーの詳細を確認してください。